Last time we looked at uncertainty, risk, and probability. We'll recap those, and move onto Game Theory.
Click below for lecture notes, slides, and links to readings. A podcast of the lecture will be available after the lecture, as will a survey of the lecture. Don't forget you can print these notes by clicking the [print_link] icons on the pages.
[print_link]
Introduction
Game theory is a branch of mathematics which deals with how people act when they must take other people's intended actions into account. The theory began in earnest with August Cournot, but really took off when John von Neumann and Oscar Morgenstern wrote The Theory of Games and Economic Behaviour. Several Nobel prizes have been awarded for the development of game theory [1, 2]. The idea is to model how one player in the game will make choices taking into account their assumptions about the other player. First though, some terminology.
Notation. Each game is described by the number of players it has, the strategies they choose to undertake or might choose to undertake, and the payoffs the players receive for a given outcome.
The theory of games looks for equilibrium (sometimes a Nash equilbrium, after Dr John Nash). This equilibrium is reached when both players play their best response to one another.
Definition (Best response). Player 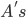 strategy
strategy 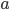 is a best response for
is a best response for 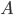 against player
against player 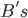 strategy
strategy 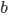 if
if 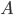 cannot do better by playing another other strategy, once
cannot do better by playing another other strategy, once 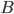 plays
plays 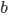 .
.
Definition (Nash Equilibrium). A set of strategies 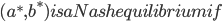 a^{*}
a^{*}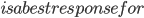 A
A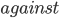 b^{*}
b^{*}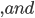 b^{*}
b^{*}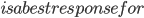 B
B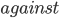 a^{*}$$.
a^{*}$$.
Example (Prisoner's Dilemma)
We'll discuss the PD in class with a demonstration, but this picture should tell you everything you need to know about it, actually. This movie provides a great explanation of it as well.
We'll also work through a mathematica demonstration about this example.
Related articles
- Vote Now on the Prisoner's Dilemma Contest
- Logic of Life - Chapter 2: Game Theory isn't Always about the Games We Play
- Game Theory.net pedagogical website

