Image via Wikipedia
[print_link]
Last time we looked at the history of game theory and the components of any game: players, strategies, and payoffs. We also discussed the first equilibrium concept we are going to see: the Nash equilibrium.
The prisoner's dilemma
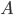and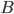 
, who have been caught in the act doing something illegal. The two suspects are put in different cells, where they can't communicate, and they are given the following set of choices by the police officer, who withdraws and lets them choose.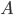's strategies are summarised on the rows, and player 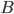's strategies are summarised in the columns. The matrix allows us to glance and see the payoffs from each strategy by each player in one simple box. Think of the matrix as the user interface for the game, kind of like the desktop on a computer. The payoffs look like this:Prisoner B Stays Silent |
Prisoner B Betrays |
|
|---|---|---|
Prisoner A Stays Silent |
Each serves 6 months |
Prisoner A: 10 years Prisoner B: goes free |
Prisoner A Betrays |
Prisoner A: goes free Prisoner B: 10 years |
Each serves 5 years |
What's the Nash equilibrium of this game?
The Nash equilibrium, recall from the last lecture, is defined as
Definition (Nash Equilibrium). A set of strategies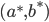 
is a Nash equilibrium if 
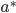is a best response for against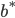 
, and 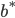is a best response for 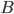against .
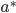See chapter 6 of the course textbook for more on the history of the Nash equilibrium concept. Or, click here or here.
So, begin with the bottom left hand box, say. Player 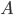will go free, but player will spend 10 years in prison. Not cool for , because he can increase his payoff from the game by moving to a strategy of telling the authorities everything, so he will play the 'betray' strategy.
The same goes for player . If both betray, they both end up doing 5 years, but if they trusted one another, they would only serve 6 months on a misdemeanour charge.
A process of elimination leads us to the bottom left hand corner of the matrix, which is where both suspects confess and get 5 years each. This is the Nash equilibrium, because for both players, there is no incentive to deviate from this strategy, taking the strategy of the other player into account.
The sad thing is for this game, the Nash equilibrium is not actually the best outcome for each player individually---that would be each staying silent. This is called the 'global optimum', but it is not stable---the local optimum of both betraying is stable, and so that is the solution to the game.
We can look at the prisoners' dilemma in extensive form as well, where we write out each sequence of decisions as branches of a tree, which lead to different payoffs at the end of the branches. This is a really useful way of discovering subgames, which I'll talk about in the next lecture. I'll use a Mathematica demonstration to show you what I mean by extensive form games in class.
Next we'll move on to consider the Tragedy of the commons.
First discussed in 1968 by Garret Hardin (see his article here), the tragedy of the commons describes a dilemma
"in which multiple individuals acting independently in their own self-interest can ultimately destroy a shared resource even where it is clear that it is not in anyone's long term interest for this to happen" [1].
We can apply the theory of the tragedy of the commons to talk about overpopulation, pollution, and other areas of resource management in economics.
In the next lecture, tomorrow, we'll talk about
- Sequential Games
- Subgame Perfection
- Terrorism
- Incomplete Information
Related articles
