Image by Getty Images via Daylife

This is the second part of the course, where we look at strategic behaviour under uncertainty. Lectures one, two, three, and four were all about establishing the theory of demand under certain conditions. We don't live in a world of certainty, but its exact opposite, so we must change the theory to account for the presence of the unknown in economic life. We have not been too successful at this, but the theory remains, and we will learn it.

The mainstream theory of how we deal with choice under uncertainty and our interactions with others is built on probability theory. 

Definition (Probability). The probability of an event occurring is the relative frequency with which it occurs. 

Example. Toss a coin a large number of times, and the likelihood you get Heads will be 1/2. Roll a dice a large number of times, and you will roll a 6 on average 1/6 of the time.

Definition (Expected Value). The expected value of a game with several uncertain outcomes is the size of the prize the winner will get, on average. It is the average outcome from an uncertain gamble. 

Example. In a 2-player game of tossing a coin and predicting whether it comes up heads (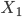) or tails (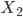), with payoffs to each player being +1 and -1 respectively, then the expected value of the game is 

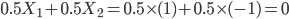
So in this game, neither player would make out too well over time. 

Risk Aversion. People prefer less risk, especially when the stakes are quite high. The reason is the interaction of the potential payoff (the 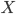above) and the probability of obtaining that payoff. We say there is diminishing marginal utility from the consumption of further and further amounts of risk. In terms of pricing risk, we can look at Figure 1 below:

Here we see the utility associated with a certain level of risk is concave to the origin---meaning when things get more risky, the person is less likely to derive a correspondingly high utility from that risky situation. If the person were truly risk-neutral, then they would pay for a gamble, but they don't, because for them, the bet simply is not worth it. As the HET site writes:

Notice by comparing points D and E in Figure 1 that the concavity of the elementary utility function implies that the utility of expected income, u[E(z)] is greater than expected utility E(u), i.e. u[pz₁ + (1-p)z₂] > pu(z₁) + (1-p)u(z₂). This represents the utility-decreasing aspects of pure risk-bearing. We can think of it this way. Suppose there are two lotteries, one that pays E(z) with certainty and another that pays z₁ or z₂ with probabilities (p, 1-p) respectively. Reverting to our von Neumann-Morgenstern notation, the utility of the first lottery is U(E(z)) = u(E(z)) as E(z) is received with certainty; the utility of the second lottery is U(z₁, z₂; p, 1-p) = pu(z₁) + (1-p)u(z₂). Now, the expected income in both lotteries is the same, yet it is obvious that if an agent is generally averse to risk he would prefer E(z) with certainty than E(z) with uncertainty, i.e. he would choose the first lottery over the second. This is what is captured in Figure 1 as u[E(z)] > E(u).

We have many ways to cope with this type of risk, but the three most common are:

1. Insurance
2. Diversification
3. Options

We'll go through each of these in class with a demonstration about the market for used cars. 

Not that there is always and everywhere a fundamental uncertainty---we can't know what we don't know. For more on this, see The Black Swan by Nassim Taleb, or my review of that book here. 

Related articles

• Black Swan Quote Of The Day
• Outliers
• The Turkey Problem
• Confirmation Bias
• Nassim Taleb, Black Swan Author, To Participate in JSM Panel Discussion
• Paint it Black
• Black SwaNS Everywhere