Consumer theory – Stephen Kinsella

List

Economics for Business Lecture 18: Markets and the Macroeconomy, Part 2

19/11/2008 | Stephen Kinsella | Teaching, EC4004 | Consumer theory, Economic, Exchange rate, Labour economics, Model, Real versus nominal value, Saving, Substitution Effect

Last week we saw the first parts of a micro-founded macroeconomy. Following Barro, chapter 6, we defined four markets: the product market, the labour market, the money market, and the bond market. We assume there was only one type of economic agent: households.

Firms are only 'placeholder' entities which consist of rental agreeements between households, who actually own all the capital, 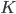and labour, . Households rent capital to firms at a rate 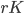, and labour at a rate 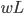. The firm produces output 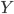according to 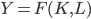, our simple production function. The total supply of labour is assumed to be used in production, so 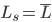, and the total capital available is used in production, thus 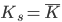. Money is present in the system only as a lubricant,or medium of exchange: agents hold it temporarily while trying to get more consumption rather than for it's own sake. Money is measured in nominal terms.

The price level, 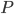, allows us to deflate nominal values to real values. So, 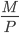is the real exchange rate of goods for money, so 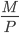will purchase you 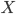units of the good. The real wage rate, 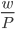, in equilibrium, is equal to the marginal productivity of labour, 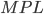. Similarly, the real return on capital, 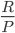, is equal to the marginal product of capital, .

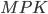Now, each market is assumed to find itself in equilibrium, so the budget constraint faced by the households is going to come from it's income in each of the four markets.

Market | Nominal Income | Real Income

Product Market | Profit, |

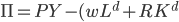
Labour Market | Wages, |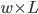

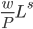
Capital Market | Rent, |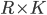

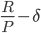
Bond Market | Interest, |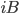

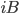
Now, this economy is populated by the households. The households want to maximise their total incomes for consumption given the price level, 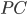, subject to the budget constraints imposed by their holdings of their total assets (in this particular period).

The household's total income is given by

Total Household nominal income = nominal profit + nominal wage income + nominal rent income + nominal rent income.

or:

Household nominal income = .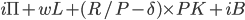

Now, Barro defines savings as the change in assets over time. The assets in this economy are money, 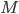, bonds, 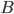, and capital, 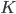, so the nominal value of assets = 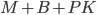. The change in the nominal value of the assets, or the savings, will look like

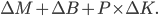
Assuming the change in money is zero, then we have that nominal saving is the difference between nominal income and nominal consumption.

The household budget constrain in nominal terms is given by

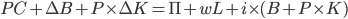This equation tells us the household in each period has to balance their consumption and their saving against their incomes from the various sources.

The real valued version of the budget constraint is given by

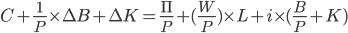
Or, in words: consumption + real saving = real income.

Again, in equilibrium, the 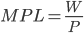, and .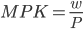

Consumption and Saving

Now, the previous section spent itself working out the details of the equilibrium macroeconomic model.

We'll study the household's choice of consumption profiles over time. The household has to choose how much consumption and real saving to do in each period. This amount, consumption plus saving, has to equal the amount of real income in the period.

We know from the equation above that the real budget constraint is:

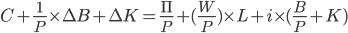
Now, we want to extend it over time.

Starting at year 1, the year which follows year 0 (I know it sounds stupid, but it'll make the equation easier to read, so bear with me), the budget constraint will be

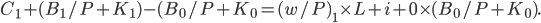
In year 2, the budget constraint will be

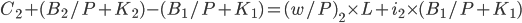Now, the important point to note here is to see the relationship between year 1 and year 2. Combining the two years using the relationship between bonds and price levels, we have

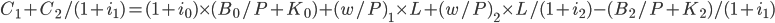This two year budget constraint is discounted into the present by the value of the interest rate, 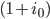, which divides the value of, say, consumption, in period 2 by a discount factor to obtain it's present value. The basic idea is consumption tomorrow is less highly valued than consumption today. We would like to measure how much tomorrow's consumption is worth in today's terms. We use the discount factor to achieve this.

Using the discount factor approach, we can derive (see Barro pages 157-158) an expression for the present value of consumption being equal to the present value of the source of funds minus the present value of assets at the end of the second year.

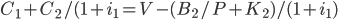where .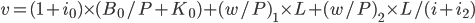

We can use this equation to examine changes in consumption and savings behaviours of households over time, using the familiar income and substitution effects.

Income and Substitution Effects.

You have studied income and substitution effects in Prof. Dineen's class last semester.

The household wants to choose a path of consumption over the periods it is alive which maxmises consumption, given the budget constraint. The household can change the profile of it's consumption, choosing to consume less today and more tomorrow, or vice versa. The interest rate, 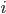, allows the household to choose which course of action to take. The higher the discount factor, 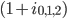, the higher the reward for waiting. There is an intertemporal substitution effect brought on by a changing interest rate.

Take, for example, the SSIA scheme. This was a scheme funded by the Irish government which gave €1 for every €4 invested in a particular savings scheme, the SSIA. The savings scheme was very popular, and many people were drawn into the scheme. Because people were saving more, their consumption would go down, and they would trade off present for future consumption because of this.

This is exactly what happened, albeit in a growing economy. More details on an economic analysis of the SSIA scheme can be found here.

In our model, the household responds to a change in the interest rate (and, obviously, the discount factor), by changing it's consumption and savings mix over time. In each period, consumption + real saving must equal real income. Because the savings rate is dependent on the interest rate, when 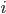rises, the savings rate goes up, and the level of consumption drops.

The income effect from a change in the interest rate comes when interest earned on bonds issued in the previous period comes back--when the SSIA matured, or, in period 1, 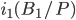. The ownership of capital, 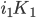, gives us the rental income received on these assets at the end of the first year.

Putting these two effects together, assuming an increase in the interest rate, the substitution effects sees consumption in the first period drop, in favour of consumption in the next period. The income effect sees an offset in the substitution effect, because if real income rises, then consumption will rise with it and 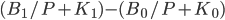will fall. So there is a tradeoff.