 Image via Wikipedia
Image via WikipediaAttention conservation notice: apologies for all the 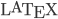 code/typos/stupidity here, I'm working on some notes on Limit Orders for a paper I'm writing. Any comments most welcome.
code/typos/stupidity here, I'm working on some notes on Limit Orders for a paper I'm writing. Any comments most welcome.
A limit order is an instruction to trade a specific quantity of an asset at a specified price, or a better price. The order is an ex-ante pre-commitment 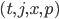 made on a date
made on a date 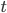 to trade up to a given amount
to trade up to a given amount 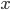 of an asset
of an asset 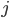 at a prespecified limit price
at a prespecified limit price 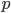 . The order is in force until filled or cancelled, so unfilled orders accumulate in an limit order book (Kyle, 1989).
. The order is in force until filled or cancelled, so unfilled orders accumulate in an limit order book (Kyle, 1989).
Limit orders differ from standard market orders, which are requests to trade immediately at the best available price in the market. In a limit order setting the order execution is always filled at the limit price set by the buyer or seller. In limit orders, price priority holds, which means the limit orders offering better terms of trade (buyers buying higher, sellers selling lower) execute ahead of limit orders at worse prices. Time priority can also hold, where at each price 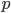 , older limit orders are executed ahead of newer ones in a queuing system which thus rewards first movers who give up liquid positions to allow the LOOM to work more effectively. The price and time priorities may be taken together to define a probability distribution over execution timing. The notion of equilibrium in limit order markets is different to other continuously clearing markets, because buyers arrive and trade asynchronously in a limit order market, so there is no unique market-wide `market-clearing' price, except in degenerate cases. Rather, there is a sequence of bilateral transaction prices at which endogenously matched pairs of investors choose to trade over time.
, older limit orders are executed ahead of newer ones in a queuing system which thus rewards first movers who give up liquid positions to allow the LOOM to work more effectively. The price and time priorities may be taken together to define a probability distribution over execution timing. The notion of equilibrium in limit order markets is different to other continuously clearing markets, because buyers arrive and trade asynchronously in a limit order market, so there is no unique market-wide `market-clearing' price, except in degenerate cases. Rather, there is a sequence of bilateral transaction prices at which endogenously matched pairs of investors choose to trade over time.
A limit order to buy 100 shares can be filled at \$47.50 or below. A limit order to sell at \$50.25 can be filled at \$50.25 and above. The existence of the limit order is independent of having anyone to actually trade to fulfil the order. As time passes, one might not be able to fill the order. There several advantages to limit order markets. The first is the ability to obtain a better price within tolerant risk boundaries as defined or perceived by the buyer or seller. The second is the discrete nature of each trade: a limit order to buy simply means you specify how much of something you want, and and how much you are willing to pay for it, and vice versa for the supplier. Both demand and supply are discrete functions of price. Any combination of these orders in a specific time and place gives rise to a limit order only interupted market where the orders are matched up for execution (Osborne, 1977, Chapter 2) is the classic exposition of LOOM). The third advantage of the LOOM structure is it's simplicity in execution: one can easily define a greedy algorithm for such a market.
The execution of a simple market algorithm will always generate either a highest bid (if there are no sell orders), a lowest offer (no buy orders), a quote, (bid and offer but no transaction) or a transaction at a unique price. The only requirement is the orders have finite price limits on them. The market algorithm puts the orders to buy and sell in ranks, applies an ambiguity rule to ensure there is a unique price.
And this algorithm will look something like this:
Assigning transactions Algorithm
1. Begin. Sort buyers in descending order by the suggested price per unit.
2. Sort sellers in ascending order by the requested price per unit.
3. Traverse the two lists from top to bottom, and perform transactions while maintaining the total amount sold equal to the total amount bought. Repeat.
4. Stop when the offered price in the buyer's list is lower than the requested price in the seller's list.
Next bit of the paper---simulate this thing, and see what happens. Then apply it somewhere cool
Related articles

